12. Central Limit Theorem [Optional]
Central Limit Theorem
The information from here until the end of the Gaussian Distributions lesson is optional.
This part of the lesson gives insight into where the Gaussian distribution comes from. If you would like to learn about the theory behind Gaussian distributions, then read on! Otherwise, you can move on to the Robot Localization lesson.
What is the Central Limit Theorem?
The central limit theorem is quite interesting. It says that if you take large enough samples from a population and then calculate the sample means, these means will be normally distributed. The theorem should hold as long as the sample size is large enough and the variable in question is independent and random.
This might all sound theoretical at this point. So in the next part of the lesson, we'll use Python to show you how the theorem works.
A Population
A population consists of all of the values of a data set. For this lesson, we're going to use a data that looks like this:
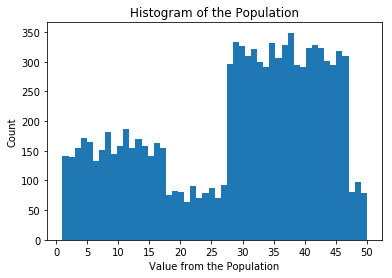
Population Distribution
For example, the value 15 shows up in the population about 160 times. The value 50 shows up in the population about 70 times. In total, this population has 10,000 data points.
Consider randomly grabbing 100 data points from this distribution. Call these 100 data points a sample. Then calculate the mean value of the sample. If you did this random sampling over and over again, the mean values would have a Gaussian distribution.
It's amazing that a population distribution that does not look Gaussian at all becomes Gaussian as you take the mean of many samples.
In the following part of the lesson, we'll show you how this works using Python code.